Please scan the frequently asked questions below or enter keywords in the search field to right and press the search button to find webpages, whitepapers, presentations, knowledge bases and many other resources located throughout our website. If you are looking for specific documentation on Cranium or Synapse, please go to the Documentation page and use the search capabilities there. And of course, please contact us if you cannot find answers to your questions.
Cranium and Synapse can estimate many properties of many chemicals and mixtures. We constantly review the literature for new data, new parameters and new estimation techniques. We are also increasingly developing our own estimation techniques. However, there are many, many chemicals and even more mixtures in the universe. We cannot estimate everything - not yet. The table to the right lists the estimation techniques contained in the latest release of our MKS Core Knowledge Base.
The best answer to this question is "try it out". Trial versions of both Cranium and synapse can be downloaded from this website. And, as always, please contact us. We are always happy to learn about the new chemicals and mixtures people are working. We would be happy to show you how to quickly try out your estimation question.
| Property | Estimation Technique |
|---|---|
| Acentric Factor | AcF: Definition [MKS] |
| Acentric Factor | AcF: Lee + Kesler Relation [MKS] |
| Activity Coefficient, LLE - f(T,P,X) | ActC,LLE (T,P,X): UNIFAC Method [MKS] |
| Activity Coefficient, VLE - f(T,P,X) | ActC,VLE (T,P,X): DECHEMA, Margules - 500 mmHg [MKS] |
| Activity Coefficient, VLE - f(T,P,X) | ActC,VLE (T,P,X): Holmes + van Winkle, Margules - 500 mmHg [MKS] |
| Activity Coefficient, VLE - f(T,P,X) | ActC,VLE (T,P,X): Holmes + van Winkle, Margules - 760 mmHg [MKS] |
| Activity Coefficient, VLE - f(T,P,X) | ActC,VLE (T,P,X): Holmes + van Winkle, van Laar - 500 mmHg [MKS 01] |
| Activity Coefficient, VLE - f(T,P,X) | ActC,VLE (T,P,X): Holmes + van Winkle, van Laar - 760 mmHg [MKS] |
| Activity Coefficient, VLE - f(T,P,X) | ActC,VLE (T,P,X): Holmes + van Winkle, Wilson - 760 mmHg [MKS] |
| Activity Coefficient, VLE - f(T,P,X) | ActC,VLE (T,P,X): Modified UNIFAC (Dortmund) Method [MKS] |
| Activity Coefficient, VLE - f(T,P,X) | ActC,VLE (T,P,X): MOSCED [MKS] |
| Activity Coefficient, VLE - f(T,P,X) | ActC,VLE (T,P,X): UNIFAC Method [MKS] |
| Autoignition Temperature | AIT: Chen + Liaw + Kuo Method [MKS] |
| Boiling Point | Tb: Antoine Equation - PGL 2001 [MKS] |
| Boiling Point | Tb: Joback Method [MKS] |
| Boiling Point | Tb: Stein + Brown Method [MKS] |
| Boiling Point - f(X) | Tb (X): Gamma-Ideal Method [MKS] |
| Critical Compressibility | Zc: Definition [MKS] |
| Critical Pressure | Pc: Joback Method [MKS] |
| Critical Pressure | Pc: Lydersen Method [MKS] |
| Critical Pressure | Pc: Myers + Danner Technique [MKS] |
| Critical Pressure | Pc: Vapor Pressure Extrapolation [MKS] |
| Critical Pressure | Pc: Wilson + Jasperson Method [MKS] |
| Critical Pressure - f(X) | Pc (X): Chueh + Prausnitz Method [MKS] |
| Critical Pressure - f(X) | Pc (X): Kreglewski + Kay Method [MKS] |
| Critical Temperature | Tc: Fedors Technique [MKS] |
| Critical Temperature | Tc: Joback Method [MKS] |
| Critical Temperature | Tc: Klincewicz Method [MKS] |
| Critical Temperature | Tc: Lydersen Method [MKS] |
| Critical Temperature | Tc: Myers + Danner Technique [MKS] |
| Critical Temperature | Tc: Tu Method [MKS] |
| Critical Temperature | Tc: Wilson + Jasperson Method - First Order [MKS] |
| Critical Temperature - f(X) | Tc (X): Chueh + Prausnitz Method [MKS] |
| Critical Temperature - f(X) | Tc (X): Li Technique [MKS] |
| Critical Volume | Vc: Ambrose Method [MKS] |
| Critical Volume | Vc: Joback Method [MKS] |
| Critical Volume | Vc: Lydersen Method [MKS] |
| Critical Volume - f(X) | Vc (X): Chueh + Prausnitz Method [MKS] |
| Critical Volume - f(X) | Vc (X): Li + Kiran + Lydersen Method [MKS] |
| Density, Liquid - f(T) | Den,l (T): Bhirud Technique [MKS] |
| Density, Liquid - f(T) | Den,l (T): Dippr Equation 105 [MKS] |
| Density, Liquid - f(T) | Den,l (T): GCVol Method [MKS] |
| Density, Liquid - f(T) | Den,l (T): Hankinson + Thomson [MKS] |
| Density, Liquid - f(T) | Den,l (T): IAPWS Formula 1995 [MKS] |
| Density, Liquid - f(T) | Den,l (T): Modified Rackett Equation [MKS] |
| Density, Liquid - f(T) | Den,l (T): Peng + Robinson EOS [MKS] |
| Density, Liquid - f(T) | Den,l (T): Rackett Equation [MKS] |
| Density, Liquid - f(T) | Den,l (T): Redlich + Kwong EOS [MKS] |
| Density, Liquid - f(T) | Den,l (T): Soave + Redlich + Kwong EOS [MKS] |
| Density, Liquid - f(T) | Den,l (T): van der Waals EOS [MKS] |
| Density, Liquid - f(T,P) | Den,l (T,P): Peng + Robinson EOS [MKS] |
| Density, Liquid - f(T,P) | Den,l (T,P): Redlich + Kwong EOS [MKS] |
| Density, Liquid - f(T,P) | Den,l (T,P): Soave + Redlich + Kwong EOS [MKS] |
| Density, Liquid - f(T,P) | Den,l (T,P): Thomas + Brobst + Hankinson Method [MKS] |
| Density, Liquid - f(T,P) | Den,l (T,P): van der Waals EOS [MKS] |
| Density, Liquid - f(T,P,X) | Den,l (T,P,X): Peng + Robinson EOS [MKS] |
| Density, Liquid - f(T,P,X) | Den,l (T,P,X): Soave + Redlich + Kwong EOS [MKS] |
| Density, Liquid - f(T,X) | Den,l (T,X): Hankinson + Thomson [MKS] |
| Density, Liquid - f(T,X) | Den,l (T,X): Spencer + Danner Method [MKS] |
| Density, Vapor - f(T,P) | Den,v (T,P): Ideal Gas Law [MKS] |
| Density, Vapor - f(T,P) | Den,v (T,P): Peng + Robinson EOS [MKS] |
| Density, Vapor - f(T,P) | Den,v (T,P): Redlich + Kwong EOS [MKS] |
| Density, Vapor - f(T,P) | Den,v (T,P): Soave + Redlich + Kwong EOS [MKS] |
| Density, Vapor - f(T,P) | Den,v (T,P): van der Waals EOS [MKS] |
| Density, Vapor - f(T,P,X) | Den,v (T,P,X): Peng + Robinson EOS [MKS] |
| Density, Vapor - f(T,P,X) | Den,v (T,P,X): Soave + Redlich + Kwong EOS [MKS] |
| Diffusion Coefficient, Vapor - f(T,P,X) | DiffC,v (T,P,X): Chapman + Enskog Method [MKS] |
| Enthalpy of Combustion at 298K | Hc,298: Enthalpy Difference Calculation [MKS] |
| Enthalpy of Formation, Liquid at 298K | Hf,l,298: Vapor Estimate Adjustment [MKS] |
| Enthalpy of Formation, Vapor at 298K | Hf,v,298: Joback Method [MKS] |
| Enthalpy of Fusion at Tm | Hm,tm: Joback Method [MKS] |
| Enthalpy of Vaporization - f(T) | Hv (T): Dippr Equation 106 [MKS] |
| Enthalpy of Vaporization - f(T) | Hv (T): Pitzer Correlation [MKS] |
| Enthalpy of Vaporization - f(T) | Hv (T): Tu + Liu Method [MKS] |
| Enthalpy of Vaporization - f(T) | Hv (T): Watson Relation [MKS] |
| Enthalpy of Vaporization at Tb | Hv,tb: Chen Method [MKS] |
| Enthalpy of Vaporization at Tb | Hv,tb: Joback Method [MKS] |
| Enthalpy of Vaporization at Tb | Hv,tb: Riedel Method [MKS] |
| Enthalpy of Vaporization at Tb | Hv,tb: Vetere Method [MKS] |
| Enthalpy, Liquid - f(T) | H,l (T): Trapezoid Integration Method [MKS] |
| Enthalpy, Liquid - f(T,P) | H,l (T,P): Trapezoid Integration Method [MKS] |
| Enthalpy, Vapor - f(T) | H,v (T): Trapezoid Integration Method [MKS] |
| Entropy, Liquid - f(T) | S,l (T): Trapezoid Integration Method [MKS] |
| Entropy, Vapor - f(T) | S,v (T): Trapezoid Integration Method [MKS] |
| Flammability Limit, Lower | LFL: Seaton Method [MKS] |
| Flammability Limit, Lower | LFL: Shebeko Atom Technique [MKS] |
| Flammability Limit, Lower | LFL: Shebeko Modified Technique [MKS] |
| Flammability Limit, Lower - f(X) | LFL (X): Le Chatelier Method [MKS] |
| Flammability Limit, Upper | UFL: High + Danner Method [MKS] |
| Flammability Limit, Upper | UFL: Seaton Method [MKS] |
| Flammability Limit, Upper - f(X) | UFL (X): Le Chatelier Method [MKS] |
| Flash Point, Closed Cup | Tf,cc: Affens Method [MKS] |
| Flash Point, Closed Cup | Tf,cc: Butler + Cooke + Lukk + Jameson Method [MKS] |
| Flash Point, Closed Cup | Tf,cc: Catoire + Naudet Method [MKS] |
| Flash Point, Closed Cup | Tf,cc: Hshieh Organics Method [MKS] |
| Flash Point, Closed Cup | Tf,cc: Patil Method [MKS] |
| Flash Point, Closed Cup | Tf,cc: Satyanarayana + Kakati Method [MKS] |
| Flash Point, Closed Cup - f(X) | Tf,cc (X): Catoire + Paulmier + Naudet Ideal Method [MKS] |
| Flash Point, Closed Cup - f(X) | Tf,cc (X): Catoire + Paulmier + Naudet Method [MKS] |
| Flash Point, Closed Cup - f(X) | Tf,cc (X): Liaw + Tang + Lai Method [MKS] |
| Fugacity Coefficient, Liquid - f(T,P) | Fug,l (T,P): Peng + Robinson EOS [MKS] |
| Fugacity Coefficient, Liquid - f(T,P,X) | Fug,l (T,P,X): Peng + Robinson EOS [MKS] |
| Fugacity Coefficient, Vapor - f(T,P) | Fug,v (T,P): Peng + Robinson EOS [MKS] |
| Fugacity Coefficient, Vapor - f(T,P,X) | Fug,v (T,P,X): Peng + Robinson EOS [MKS] |
| General Calculation | GenCalc: 2-Hydroxybenzoic acid solubility at 25°C [MKS] |
| General Calculation | GenCalc: Diffusion in Air (25C, 101kPa, cm2/sec) [MKS] |
| General Calculation | GenCalc: Hill Cross Sectional Area - [MKS] |
| General Calculation | GenCalc: Naphthalene solubility at 25°C [MKS] |
| General Calculation | GenCalc: Number of Oxygen Atoms [MKS] |
| General Calculation | GenCalc: Oxygen Balance Calculation [MKS] |
| General Calculation | GenCalc: Solubility in pyridine at 25°C [MKS] |
| General Calculation | GenCalc: Specific Gravity at 20°C [MKS] |
| General Calculation - f(X) | GenCalc (X): Binary Azeotrope Formed [MKS] |
| General Calculation - f(X) | GenCalc (X): Percentage of Wetted Surface Area - [MKS] |
| Gibbs Energy of Formation, Vapor at 298K | Gf,v,298: Joback Method [MKS] |
| Heat Capacity - Isobaric, Liquid - f(T) | Cp,l (T): Dippr Equation 100 [MKS] |
| Heat Capacity - Isobaric, Liquid - f(T) | Cp,l (T): IUPAC Cubic Splines [MKS] |
| Heat Capacity - Isobaric, Liquid - f(T) | Cp,l (T): Missenard Method [MKS] |
| Heat Capacity - Isobaric, Liquid - f(T) | Cp,l (T): Poling + Prausnitz + O'Connell CSP Method [MKS] |
| Heat Capacity - Isobaric, Liquid - f(T,X) | Cp,l (T,X): Ideal Molar Mixing Rule [MKS] |
| Heat Capacity - Isobaric, Liquid at 298K | Cp,l,298: Chickos + Acree Method [MKS] |
| Heat Capacity - Isobaric, Solid - f(T) | Cp,s (T): Goodman + Wilding + Oscarson + Rowley Method [MKS] |
| Heat Capacity - Isobaric, Solid at 298K | Cp,s,298: Chickos + Acree Method [MKS] |
| Heat Capacity - Isobaric, Solid at 298K | Cp,s,298: Hurst + Harrison [MKS] |
| Heat Capacity - Isobaric, Vapor - f(T) | Cp,v (T): Dippr Equation 107 [MKS] |
| Heat Capacity - Isobaric, Vapor - f(T) | Cp,v (T): Joback Method [MKS] |
| Heat Capacity - Isobaric, Vapor - f(T,X) | Cp,v (T,X): Ideal Molar Mixing Rule [MKS] |
| Heat Capacity - Isobaric, Vapor at 298K | Cp,v,298: Fixed Temperature Method [MKS] |
| Heat Capacity - Isobaric, Vapor at 298K | Cp,v,298: Joback Method [MKS] |
| Heat Capacity - Isometric, Vapor - f(T) | Cv,v (T): Ideal Gas Relation [MKS] |
| Henry's Constant (pc) in H2O - f(T) | Hpc (T): Penttilä + Dell'Era + Uusi-Kyyny + Alopaeus Method [MKS] |
| Henry's Constant (px) in H2O - f(T) | Hpx (T): Carroll + Slupsky + Mather Method [MKS] |
| Henry's Constant (px) in H2O - f(T) | Hpx (T): Fernández-Prini + Alvarez + Harvey Method [MKS] |
| LC50 96hr, Fathead Minnow | LC50,96hr,FatMn: Martin + Young Method [MKS] |
| log(Octanol/Water Partition Coefficient) | log P: Lin + Sandler Method [MKS] |
| Melting Point | Tm: Constantinou + Gani First Order Method [MKS] |
| Melting Point | Tm: Joback Method [MKS] |
| Molecular Weight | Mw: Definition [MKS] |
| Molecular Weight - f(X) | Mw (X): Definition [MKS] |
| Refractive Index, Liquid at 293K | RI,l: Lorentz + Lorenz Equation [MKS] |
| SLE, Liquidus Temperature - f(P,X) | LiqPtTmp (P,X): Gamma VLE Eutectic Method [MKS] |
| SLE, Liquidus Temperature - f(P,X) | LiqPtTmp (P,X): Ideal Eutectic Model [MKS] |
| Solubility Parameter, Dispersive | SP,d: Stefanis + Panayiotou Method, First Order [MKS] |
| Solubility Parameter, Dispersive - f(X) | SP,d (X): Ideal Volume Fraction Average [MKS] |
| Solubility Parameter, Hydrogen Bonding | SP,h: Stefanis + Panayiotou Method, First Order - Std [MKS] |
| Solubility Parameter, Hydrogen Bonding - f(X) | SP,h (X): Ideal Volume Fraction Average [MKS] |
| Solubility Parameter, Polar | SP,p: Hansen + Beerbower Method [MKS] |
| Solubility Parameter, Polar | SP,p: Stefanis + Panayiotou Method, First Order - Std [MKS] |
| Solubility Parameter, Polar - f(X) | SP,p (X): Ideal Volume Fraction Average [MKS] |
| Solubility Parameter, Total | SP,t: Definition [MKS] |
| Solubility Parameter, Total | SP,t: Fedors Technique [MKS] |
| Solubility Parameter, Total | SP,t: Three Term Definition - Data [MKS] |
| Solubility Parameter, Total | SP,t: Three Term Definition [MKS] |
| Speed of Sound, Liquid - f(T) | SpSnd,l (T): Peng + Robinson EOS [MKS] |
| Speed of Sound, Vapor - f(T,P) | SpSnd,v (T,P): Peng + Robinson EOS [MKS] |
| Surface Tension, Liquid - f(T) | SurfTn,l (T): Brock + Bird Method [MKS] |
| Surface Tension, Liquid - f(T) | SurfTn,l (T): Dippr Equation 106 [MKS] |
| Surface Tension, Liquid - f(T) | SurfTn,l (T): Sastri + Rao Method [MKS] |
| Surface Tension, Liquid - f(T) | SurfTn,l (T): Somayajulu [MKS] |
| Surface Tension, Liquid - f(T,X) | SurfTn,l (T,X): Molar Average [MKS] |
| Thermal Conductivity, Liquid - f(T) | ThrmCnd,l (T): Dippr Equation 100 [MKS] |
| Thermal Conductivity, Liquid - f(T) | ThrmCnd,l (T): Mallan + Michaelian + Lockhart Method [MKS] |
| Thermal Conductivity, Liquid - f(T) | ThrmCnd,l (T): Missenard + Riedel Method [MKS] |
| Thermal Conductivity, Liquid - f(T) | ThrmCnd,l (T): Sastri + Rao Method [MKS] |
| Thermal Conductivity, Liquid - f(T) | ThrmCnd,l (T): Sato + Riedel Method [MKS] |
| Thermal Conductivity, Liquid - f(T,X) | ThrmCnd,l (T,X): Filippov Equation [MKS] |
| Thermal Conductivity, Liquid - f(T,X) | ThrmCnd,l (T,X): Jamieson + Irving + Tudhope Correlation [MKS] |
| Thermal Conductivity, Liquid - f(T,X) | ThrmCnd,l (T,X): Power Law Relation [MKS] |
| Thermal Conductivity, Vapor - f(T) | ThrmCnd,v (T): Dippr Equation 102 [MKS] |
| Thermal Conductivity, Vapor - f(T) | ThrmCnd,v (T): Eucken Correlation [MKS] |
| Thermal Conductivity, Vapor - f(T) | ThrmCnd,v (T): Modified Eucken Correlation [MKS] |
| Thermal Conductivity, Vapor - f(T) | ThrmCnd,v (T): Stiel + Thodos Method [MKS] |
| Thermal Conductivity, Vapor - f(T,P) | ThrmCnd,v (T,P): Stiel + Thodos High Pressure Method [MKS] |
| Triple Point, Pressure | TrpPtPrs: Liquid Vapor Pressure Method [MKS] |
| Triple Point, Pressure | TrpPtPrs: Solid Vapor Pressure Method [MKS] |
| Triple Point, Temperature | TrpPtTmp: Melting Point Technique |
| Vapor Pressure, Liquid - f(T) | Pvp,l (T): Ambrose + Walton Method [MKS] |
| Vapor Pressure, Liquid - f(T) | Pvp,l (T): Antoine Equation - PGL 2001 [MKS] |
| Vapor Pressure, Liquid - f(T) | Pvp,l (T): Dippr Equation 101 [MKS] |
| Vapor Pressure, Liquid - f(T) | Pvp,l (T): Gómez-Nieto + Thodos Equation [MKS] |
| Vapor Pressure, Liquid - f(T) | Pvp,l (T): IAPWS Formula 1995 [MKS] |
| Vapor Pressure, Liquid - f(T) | Pvp,l (T): Lee + Kesler Equation [MKS] |
| Vapor Pressure, Liquid - f(T) | Pvp,l (T): Riedel + Plank + Miller Equation [MKS] |
| Vapor Pressure, Solid - f(T) | Pvp,s (T): Jones Method [MKS] |
| Viscosity, Liquid - f(T) | Visc,l (T): Dippr Equation 101 [MKS] |
| Viscosity, Liquid - f(T) | Visc,l (T): Joback Method [MKS] |
| Viscosity, Liquid - f(T) | Visc,l (T): Orrick + Erbar Method [MKS] |
| Viscosity, Liquid - f(T) | Visc,l (T): Przezdziecki + Sridhar Method [MKS] |
| Viscosity, Liquid - f(T,P) | Visc,l (T,P): Lucas Method [MKS] |
| Viscosity, Liquid - f(T,X) | Visc,l (T,X): Arrhenius Equation [MKS] |
| Viscosity, Liquid - f(T,X) | Visc,l (T,X): Kendall + Monroe Relation [MKS] |
| Viscosity, Vapor - f(T) | Visc,v (T): Dippr Equation 102 [MKS] |
| Viscosity, Vapor - f(T) | Visc,v (T): Lucas Method [MKS] |
| Viscosity, Vapor - f(T) | Visc,v (T): Reichenberg Technique [MKS] |
| Viscosity, Vapor - f(T) | Visc,v (T): Yoon + Thodos Method [MKS] |
| Viscosity, Vapor - f(T,P) | Visc,v (T,P): Reichenberg Method [MKS] |
| Viscosity, Vapor - f(T,X) | Visc,v (T,X): Wilke Equation [MKS] |
| VLE, Bubble Pressure - f(T,X) | BubPtPrs (T,X): Gamma-Ideal Method [MKS] |
| VLE, Bubble Pressure - f(T,X) | BubPtPrs (T,X): Ideal-Ideal Method [MKS] |
| VLE, Bubble Pressure - f(T,X) | BubPtPrs (T,X): Phi-Phi Method [MKS] |
| VLE, Bubble Temperature - f(P,X) | BubPtTmp (P,X): Gamma-Ideal Method [MKS] |
| VLE, Bubble Temperature - f(P,X) | BubPtTmp (P,X): Ideal-Ideal Method [MKS] |
| VLE, Bubble Temperature - f(P,X) | BubPtTmp (P,X): Phi-Phi Method [MKS] |
| VLE, Dew Pressure - f(T,X) | DewPtPrs (T,X): Gamma-Ideal Method [MKS] |
| VLE, Dew Pressure - f(T,X) | DewPtPrs (T,X): Ideal-Ideal Method [MKS] |
| VLE, Dew Pressure - f(T,X) | DewPtPrs (T,X): Phi-Phi Method [MKS] |
| VLE, Dew Temperature - f(P,X) | DewPtTmp (P,X): Gamma-Ideal Method [MKS] |
| VLE, Dew Temperature - f(P,X) | DewPtTmp (P,X): Ideal-Ideal Method [MKS] |
| VLE, Dew Temperature - f(P,X) | DewPtTmp (P,X): Phi-Phi Method [MKS] |
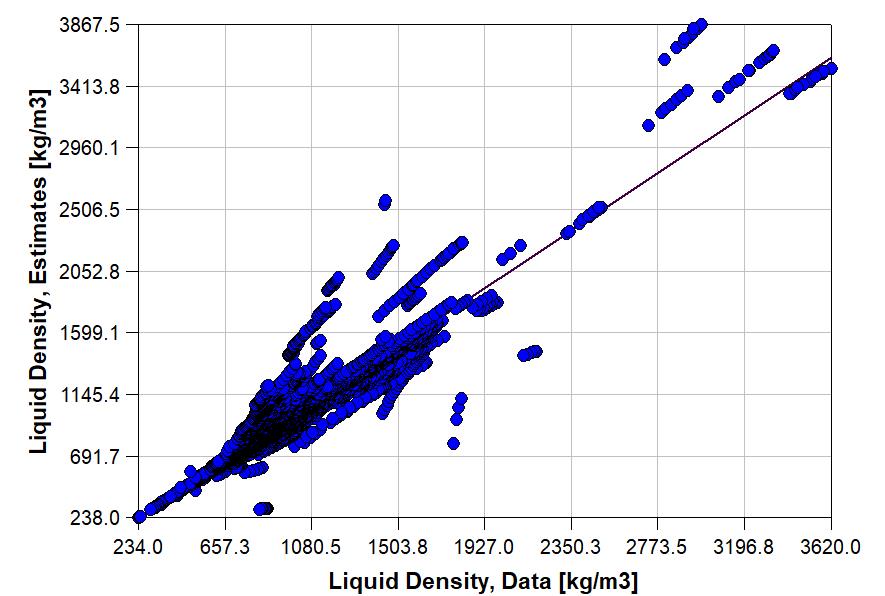
The accuracy of an estimation depends upon many factors, e.g., the chemical or mixture, the property being estimated, the temperature, pressure or composition. For example, the graph to the right shows errors for the liquid density estimated by the Rackett Equation. Overall, the average percentage error is 6.6%. Many lower molecular weight chemicals, e.g., cyclohexane, propane, 1-butanol, have estimation errors of less than 1%. Some higher molecular chemicals, e.g., methyl oleate and 1,1,2,2-tetrabromoethane, have estimation error of greater than 20%.
We routinely compile physical property data and evaluate estimation technique looking to identify accuracy and applicability rules, i.e., rules that tell you how accurate an estimation technique is for your classes of chemicals and mixtures.
However, the best answer to this question is "try it out". In only a few minutes you can use either Cranium or Synapse to generate dozens, even thousands, of physical property estimates for similar chemicals, similar mixtures or similar state conditions. Evaluating how estimation methods work for these similar problems is the best way to determine how they will work for your problem.
As the table to the right shows, both Cranium and Synapse have capabilities for data management, physical property estimation, graphing, reporting and interacting with other software programs. Synapse has additional capabilities for selecting and designing chemical structures and mixture formulations.
Very often using both Cranium and Synapse is an economical solution for a research group. Some members are typically focused on data curation, gathering and entering data from experiments, literature and other sources. Other members of the group are focused on the design of new chemical structures and formulations.| Capability | Cranium | Synapse |
|---|---|---|
| Manage Physical Property Data | ✔ | ✔ |
| Estimate Chemical Properties | ✔ | ✔ |
| Estimate Mixture Properties | ✔ | ✔ |
| Create/Edit Estimation Techniques | ✔ | ✔ |
| Create XY Graphs | ✔ | ✔ |
| Create Triangular Graphs | ✔ | ✔ |
| Select Chemicals | ✔ | |
| Design Chemicals | ✔ | |
| Select Mixtures | ✔ | |
| Design Mixtures | ✔ |
Our goal is to release a major upgrade of Cranium and Synapse every two years. These major releases typically provide you with new property estimation and product design capabilities. New major releases also often included changes that take advantage of advances in the underlying Microsoft Windows, C++ or database capabilities.
Because major releases also often include changes to the user interface and underlying software functionality, some retraining and file conversions may be needed.
Minor releases occur frequently throughout the two years between major releases. Minor releases include bug fixes and user interface optimizations.
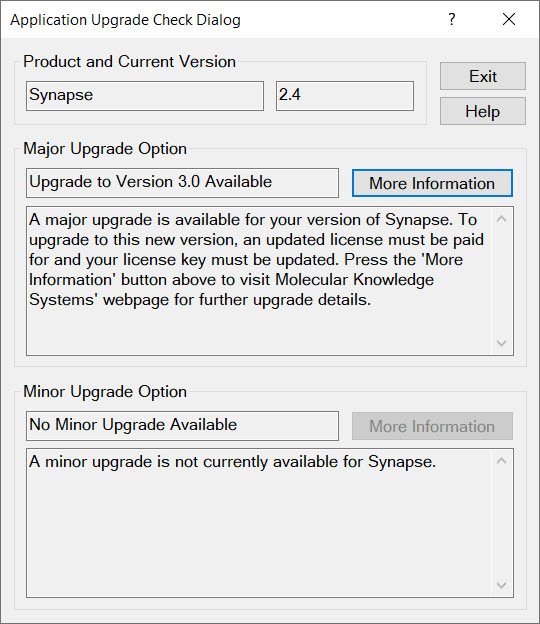
Synapse and Cranium automatically check for upgrades every time they start. (We also notify our customers by email about new releases.) If a new release is available, The Application Upgrade Check Dialog is displayed providing you with directions on how to upgrade.
One of the most powerful capabilities of Cranium and Synapse is that all estimation techniques, design functions, selection rules are first class data objects contained in Knowledge Bases, Selection Documents and Design Documents. This means that as we add new data, new estimation techniques and new example designs, you do not have to upgrade the software. You only need to copy and paste the new values into your current documents.
Cranium's capabilities make it the perfect tool for customers focused on having high quality physical property values, data values and estimates, available for their work. Some example uses include:
- A flavors and fragrances company that has created a knowledge base of all their products for quick calculation of vapor pressures and other properties.
- A pharmaceutical company that quickly examines the vapor-liquid equilibrium curves for a reactant chemical and a set of commonly used solvents.
- A solvents company that wanted to examine how structural modifications of one of their chemicals would change physical properties possibly identifying a new product.
- A research institution examining the properties of new biomass derived chemicals.
- A traditional chemicals company looking to organize, consolidate and easily diseminte decades of experimental physical property data measurements, internally developed estimation techniques and soon to be retired expert knowledge.
Synapse's capabilities make it the perfect tool for helping researchers design innovative, new chemical products. Process chemists and process engineers also find Synapse's advanced chemical selection capabilities an essential tool for identifying extraction solvents and formulation ingredients. Some example uses include:
- a fluorinated chemicals company designs new refrigerant mixtures that have good performance and low environmental impact.
- a solvents company identifies common co-solvents to blend with its premier solvents product line to achieve customer specified properties.
- a consumer products company optimizes the blend of ingredients in its cleaning products to achieve a desired evaporation rate.
- a biotech company identifies an optimal solvent for extracting a key product chemical from its fermentation broth.
- a fragrance chemicals company designs a blend of ingredients that upon evaporation gives a vapor composition having just the right blend of ingredients to give an attractive aroma.
In short, yes. Both Cranium and Synapse use a set of rules to determine which estimation techniques should be used for which chemicals and mixtures. These rules consider a chemical's molecular structure, a mixture's composition, temperature, pressure and concentration. Synapse uses and advanced "generate and test algorithm" to efficiently and exhaustively generate new chemical structures and mixture formulations.
Many of the estimation techniques used by Cranium and Synapse were developed using multiple linear regression, an simple but very powerful form of machine learning. Cranium and Synapse include regression capabilities enabling you to obtain technique parameters from new data you enter into your knowledge bases. In this manner, you can continually increase the molecular knowledge Cranium and Synapse have and even tailor that knowledge to your specific classes of chemical products.
Our founder, Dr. Kevin Joback, did his doctoral research on applying artificial intelligence techniques to the design of molecules - back in the 1980s. We guess this is the reason we do not "brag" about Cranium and Synapse being based on artificial intelligence techniques. That is the way we have been developing them since we started.
Chemical process simulators are amazing software tools. They can help you design chemical plants, optimize performance and minimize energy consumption. To accomplish these tasks, many simulators contain databanks, property estimation methods and some even allow you to enter your own molecules and data values.
As such, some people ask how does Cranium, our physical property estimation software, compare with the property estimation capabilities within their process simulator. We would hope that, just as 2 + 2 = 4 within Cranium and a process simulator, estimating the critical temperature of acetic acid by Lydersen's method should give you the same value within Cranium and a process simulator. Yes, Cranium often has more estimation techniques than a process simulator. And yes, the techniques are often more up to date. But in general, if all you need is some property estimates for a single chemical or mixture, a process simulator (or even a spreadsheet) should be good enough.
But we have always felt the real answer to the question is that Cranium and process simulators are designed for two very different goals. A process simulator's goal is to design and analyze chemical process plants, an important goal. Cranium's goal is to quickly and easily give you highly accurate estimates for dozens or even thousands of chemicals and mixtures - a more important goal. (More important because process simulators will always be able to design you a chemical given any consistent set of physical properties. However, the chemical plant will only work as hoped if it has accurate physical properties.) Also, Cranium's expert system automatically selects the best estimation technique for you, enables you quickly compare techniques, retrieve and analyze data, enter new mixtures and new molecular structures. All this in a very organized, productive and easy to use software tool - because that is what Cranium was designed to do.
To further explain our thoughts on this question, we put together the two videos to the right. These videos highlight common tasks asked of Cranium. Tasks that we believe could not be easily done by a process simulator.
We often received emails thanking us for providing our demonstration versions for free on our website. These demonstration versions, we call them "Basic Editions", have almost all the same capabilities as the full version except that you cannot save any changes.
The reason why we provide such powerful demonstration versions is that physical property estimation and chemical product design are very broad fields. We recognize that neither Cranium nor Synapse can yet estimate all chemicals or design all products. Thus, we want you to try out our software on your particular products of interest. Thus providing these demonstration versions is just one of the ways we work hard at ensuring that Cranium and Synapse productive, cost-effective tools for our customers.
We sometimes have prospective customers who say they do not mind reentering the molecular structures and physical properties needed for an estimation or the groups and constraints needed for a design. We always find that comment interesting. The chemical industry in most parts of the world is very competitive. Cranium and Synapse, the complete (paid) versions, enable capture and use the physical property knowledge your company possesses. Companies that take advantage of this knowledge will be able to develop new products and new applications must faster than their competitors and thus gain great advantage in the market place. As the old saying goes "penny wise but pound foolish".
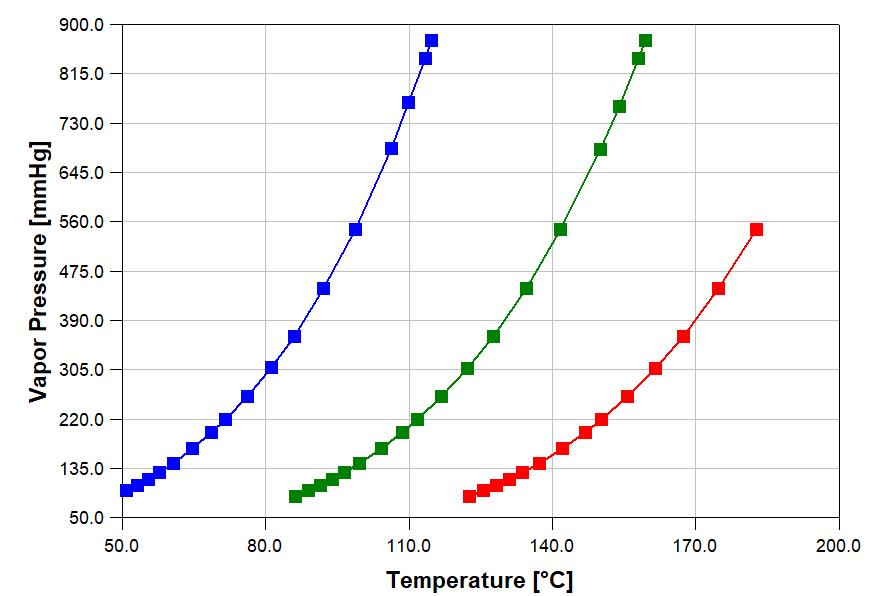
Case Study: Disulfide chemicals are often used for catalyst activation and furnace tube passivation. Dimethyl disulfide is the most commonly used chemical for these processes. It has the advantage of high sulfur content, good decomposition temperature range and simple decomposition products, i.e., methane, that do not cause unwanted coking. However, dimethyl disulfide does have a high vapor pressure, unpleasant odor and a very low flash point.
In this case study, we used Cranium to examine the properties of dimethyl disulfide and other alkyl disulfides. The specific properties investigated were melting point, vapor pressure, flash point and sulfur content. The case study shows how to build a tailored knowledge base, evaluate estimation techniques and generate XY graphs. Most importantly, the case study shows how Cranium and Synapse can expand and grow for each new problem you solve and retain this knowledge for future use.
We recognize that often you need a physical property value because you are working on something else, e.g., simulating a distillation column, using CFD software to model the dispersion of a fragrance in air, sizing a pressure safety valve. As such, both Cranium and Synapse can export physical property data and estimates into more than a dozen third-party formats. Some of these formats are:
| ASPEN Input File | CHEMCAD Neutral File | Chemical Structure Images |
| DIPPR Database Format | MATLAB Class Definition | MKS JSON File Format |
| Mol File Format | ProSim Simulis Format | SD File Format |
| AVEVA SimCentral Format | ioMosaic SuperChems File | UniSim File Format |
Of course all molecular structures, values, tables and graphs can be copied and pasted from Cranium or Synapse into other programs running on Microsoft Windows.
Many companies have expended a considerable amount of money, time and resources to measure and compile physical property data for their chemicals of interest. Product knowledge also often takes years of experience to obtain, e.g., application temperature limits, chemical compatibility, etc. Many companies have even developed estimation techniques and applicability rules tailored for their specific chemicals.
Both Cranium and Synapse can capture this physical property knowledge, organize it for easy retrieval, preserve it for future use and disseminate to reports, spreadsheets and other technical software packages. But in addition to these essential tasks, both Cranium and Synapse can help you unlock the true value contained in these data. The value gained by a better understanding of your current chemicals and help in designing innovative, new chemical products.
Cranium and Synapse can help you retain and exploit your physical property knowledge by:
- Enabling all data to be associated with accuracies, source references, comments, original units of measure, and quality rankings.
- Providing powerful tools for data absorption from printed material, graphs, databases and process simulation software databanks.
- Validating entered data against best-in-class physical property estimation techniques. A quality ranking can be assigned to each entered datum.
- Capturing expert applicability rules within tailored physical property estimation techniques.
- Disseminating physical property knowledge to word processors, spreadsheets, process simulation software, mathematical analysis tools and equipment design programs.
Molecular Knowledge Systems is continually adding chemicals, mixtures and physical property data to its knowledge bases. The main goal of this effort is to provide a data compilation to be used for estimation technique evaluation and development. Thus, only high quality, critically evaluated, experimental data are included in these compilations. The majority of data we compile are taken from their original technical literature sources.
As new data is entered into a knowledge base, Cranium and Synapse compare them against:
- standard physical property limits
- previously entered experimental data
- estimates generated from expertly selected techniques
Data are then designated as Active, Passive or Rejected. Even if a data value is rejected, you can still use Cranium's and Synapse's Edit All Data functionality to examine its value.
Of equal importance to compiling high quality data, is documenting the source of such data. This is why every document used by Cranium and Synapse has a Reference chapter. We record the reference for every entered datum. A reference whose details are stored for quick review in the Reference chapter.
Molecular Knowledge Systems has worked on numerous, diverse consulting projects. (See the table to the right and some descriptions on our Consulting page.) The key unifying theme is all these projects is the importance of physical properties and the importance of using physical property relationships to innovate new chemicals and mixtures.
We are always happy to talk about physical properties. So, if you have a project in mind, please call us to discuss if our expertise could be of assistance.
| Artificial Blood | Refrigeration Lubes | Degreasing Solvents |
| Non-MMH Rocket Fuels | Aircraft Deicing Fluids | MeCl2 Replacement |
| Jet Fuel Additives | Sonar Fill Fluids | Phase Change Materials |
| Hydraulic Energy Storage | Windshield Washer Fluid | CO2 Absorption Solvents |
| Liquid Extraction Solvents | Soil Consolidants | Paint Strippers |
| Helium Applications | Tailings Runoff Prevention | Heat Transfer Fluids |